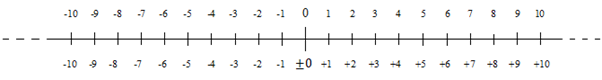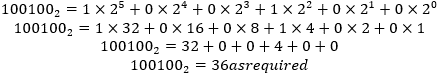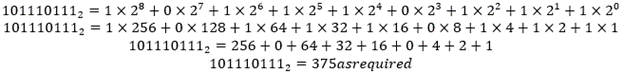Probleme und ihre Lösungen
1. Zeichnen Sie einen Zahlenstrahl mit ganzen Zahlen von -10 bis +10.
Lösung:
2. Addieren Sie die folgenden Binärzahlen im 8-Bit-Zweierkomplement: 1010102 und 11112.
Lösung:
3. Verwenden Sie nur den Zweierkomplement-Ansatz in 8 Bits, um die Binärzahl 11112 von der Binärzahl 1010102 zu subtrahieren.
Lösung:
101010 im 8-Bit-Zweierkomplement ist 00101010.
1111 in 8 Bit ist 00001111.
Die gesamte Invertierung von 00001111 in 8 Bits ergibt 11110000.
Die Addition von 1 zu 11110000 ergibt 11110001.
Bei der Subtraktion im Zweierkomplement werden die positiven und negativen Zahlen des Zweierkomplements wie folgt addiert:
Der letzte Übertrag von 1 wird bei der Zweierkomplementsubtraktion verworfen.
5. Teilen Sie 36,37510 durch 100010 im Dezimal- und im Binärformat und vergleichen Sie die Ergebnisse.
Lösung:
Es wird eine Wiederherstellungsteilung verwendet.
Dezimalteilung durch Vierer:
Die Antwort ist 36 10 Rest 375 10 .
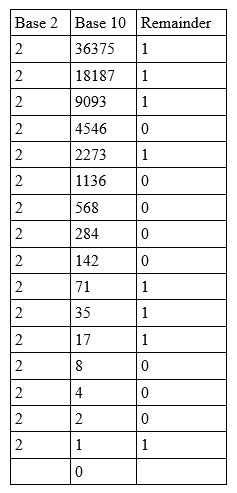
Die 36.375 10 Ganzzahl muss wie folgt in Basis 2 umgewandelt werden:
Die Reste von unten gelesen: 36.375 10 = 1000111000010111 2 .
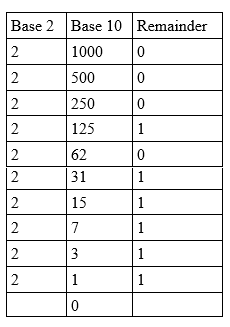
Der 1000 10 Ganzzahl muss wie folgt in Basis 2 umgewandelt werden:
Reste von unten lesen: 1000 10 = 1111101000 2 .
Als nächstes 1011000100110111 2 teilt 1111101000 2 durch lange Division (wiederherstellende Division) seit 36.375 10 = 1011000100110111 2 und 1000 10 = 1111101000 2 (binäre Division in zehn Bits):
Die Division beginnt tatsächlich beim elften Bit des Dividenden, da die ersten zehn Bits des Dividenden kleiner als der Divisor sind. Die Antwort ist 100100 2 Rest 101110111 2 .
Zum Vergleich der Ergebnisse sollte nun gezeigt werden, dass die ganzen Zahlen der Quotienten gleich sind und die Reste gleich sind. Das heißt, es sollte gezeigt werden, dass 36 10 = 100100 2 und 375 10 = 101110111 2 .
6. Verwenden Sie 8 Bits Ihrer Wahl, um die logischen Funktionen UND, ODER, XOR, Invertieren, Rechtsschieben, Linksschieben, Rechtsdrehen und Linksdrehen zu veranschaulichen. Jedes Byte sollte eine Mischung aus Einsen und Nullen haben.
Lösung:
- a) Schreiben Sie den numerischen Code für das ASCII-Zeichen Null im Hexadezimal-, Binär- und Dezimalformat.
b) Schreiben Sie den numerischen Code für das ASCII-Zeichen „1“ im Hexadezimal-, Binär- und Dezimalformat.
c) Schreiben Sie den numerischen Code für das ASCII-Zeichen „A“ im Hexadezimal-, Binär- und Dezimalformat.
d) Schreiben Sie den numerischen Code für das ASCII-Zeichen „a‘“ im Hexadezimal-, Binär- und Dezimalformat.
Lösung:
a) „0“: 30, 00110000, 48
b) „1“: 31, 00110001, 49
c) „A“: 41, 001000001, 65
d) „a“: 61, 001100001, 97
8. Wandeln Sie 49,4910 in die Basis zwei um. Konvertieren Sie Ihr Ergebnis in das IEEE 32-Bit-Gleitkommaformat.
Lösung:
Die Formen 49.4910, 49 und .49 werden unterschiedlich in die Basis 2 umgewandelt.
Konvertieren von 49:
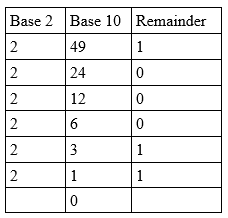
∴ 4910 = 1100012 ab dem Ende der letzten Spalte gelesen.
Konvertieren von .49:
.49 x 2 = 0,98 erstes Bit ist 0
.98 x 2 = 1,96 Sekundenbit ist 1
.96 x 2 = 1,92 drittes Bit ist 1
∴ .49 10 = 110 2 Lesen Sie von oben in der letzten Spalte.
Also 49,49 10 = 110001,110 2
110001.110 2 = 1,10001110 x 2 +5 in der Standardform der Basis zwei
Die „1.“ Der Signifikand 1,10001110 wird im Ergebnis nicht angezeigt, es wird jedoch davon ausgegangen, dass er vorhanden ist.
Für den Exponenten 127 10 stellt Null dar. Dies bedeutet, dass der Index (Potenz) von 5 ist 10 von 2 5 wird zu 127 addiert 10 . Das ist:
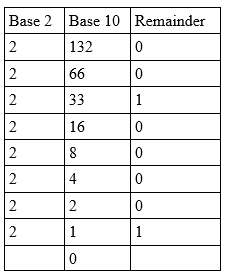
127 10 + 5 10 = 132 10
132 10 muss zur Basis zwei umgewandelt und dann in das Feld für den Exponenten eingepasst werden.
Also 132 10 = 10000100 2
10000100 2 hat 7 Bit. Der Exponent beträgt acht Bit. 10000100 2 hat acht Bits und das ist in Ordnung.
49,49 10 ist positiv, daher ist das Vorzeichenbit 0. Im 32-Bit-Gleitkommaformat 49,49 10 = 110001,110 2 Ist:
0 10000100 10001110000000000000000
- a) Wie unterscheidet sich das IEEE 64-Bit-Gleitkommaformat vom 32-Bit-Format?
b) Geben Sie die beiden zusammenhängenden Gründe an, warum das 64-Bit-Format als doppelte oder höhere Präzision gegenüber dem 32-Bit-Format beschrieben wird.
Lösung:
- – Es gibt 64 Bits zur Darstellung einer Zahl, nicht 32.
– Nach dem Vorzeichenbit folgen 11 Bits für die Exponentenzahl.
– Die Exponentenzahl für den Nullindex (2 0 ) ist 1023 10 = 01111111111 2 .
– Auf die elf Bits folgen 52 Bits für den expliziten Signifikanten.
– Es verfügt über einen größeren Zahlenbereich als das 32-Bit-Format. - Der Grund dafür, dass das 64-Bit-Format im Vergleich zum 32-Bit-Format als doppelte oder höhere Genauigkeit beschrieben wird, liegt darin, dass das Intervall zwischen zwei aufeinanderfolgenden gemischten Brüchen, die beim 64-Bit-Format durch zwei aufeinanderfolgende ganze Zahlen begrenzt werden, kleiner ist als das entsprechende 32-Bit-Formatintervall. Außerdem gibt es für das 64-Bit-Format mehr mögliche gemischte Brüche zwischen zwei begrenzten ganzen Zahlen als entsprechend für das 32-Bit-Format.