Kapitel 3: Binärzahlenoperationen im Mikroprozessor
3.1 Einführung
In einem Computer werden arithmetische Operationen in 8 Bit, 16 Bit, 32 Bit oder 64 Bit ausgeführt. Eine Zahl wie 3 im Binärformat ist 11. Wenn die Operation in 8 Bits ausgeführt werden soll, wird dies als 00000011 betrachtet; davor stehen 0 Nullen.
Bei einer Binärzahl wie 10000101 ist das höchstwertige Bit das Bit ganz links. In diesem Fall ist es 1. Das niedrigstwertige Bit ist das äußerste Bit rechts, das immer noch 1 ist, für die Zahl. Das höchstwertige Bit wird als MSB abgekürzt. Das niedrigstwertige Bit wird als LSB abgekürzt.
Die binäre Ziffer wird als BIT abgekürzt und einfach als Bit geschrieben. In der Zahl 10010011 ist jede Eins oder Null ein Bit. Eine Gruppe von vier Bits wird Nibble genannt. Eine Gruppe von acht Bits wird als Byte bezeichnet. Ein Byte besteht aus zwei Halbbytes. Das niedrigere Nibble ist das Nibble für das LSB und das höhere Nibble ist das Nibble für das MSB.
Eine Gruppe von 8 Bits, 16 Bits, 32 Bits oder 64 Bits wird als Wort bezeichnet, solange diese Gruppe Informationen übermittelt, die über die bloße Angabe einer Zahl hinausgehen. Die Gruppe wird beispielsweise als Wort bezeichnet, wenn es sich um eine Low-Level-Anweisung im Computer handelt. Es gibt auch ein 24-Bit-Wort, das heute jedoch nicht mehr häufig verwendet wird.
Endianness bezieht sich auf die Reihenfolge, in der die Bytes ein Wort bilden. Betrachten Sie das 24-Bit-Wort – 100100001111010100100010. Dieses Wort besteht aus drei Bytes:
10010000 11110101 00100010
Das höchstwertige Byte ist das am weitesten links stehende Byte. Wenn das Byte ganz links das höchstwertige Byte und das Byte ganz rechts das niederwertigste Byte ist, spricht man von der Big-Endian-Darstellung des Wortes. Die Little-Endian-Darstellung ist das Gegenteil.
Der Computerspeicher besteht aus einer Reihe von Zellen, und jede Zelle enthält ein Byte. Die erste Zelle im Speicher des Computers ist für Byte 0, die zweite für Byte 1, die dritte für Byte 2 und so weiter. Bei Big Endianness und für das vorherige Wort wird das höchstwertige Byte in Zelle Byte 0, das mittlere Byte in Zelle Byte 1 und das niedrigstwertige Byte in Zelle Byte 2 gespeichert. Dies bedeutet, dass sich in der unteren Speicherzelle mehr signifikante Bytes befinden.
Das vorherige 24-Bit-Wort kann in umgekehrter Reihenfolge der Bytes wie folgt geschrieben werden:
00100010 11110101 10010000
Jetzt befindet sich das niedrigstwertige Byte ganz links und das höchstwertige Byte ganz rechts. Wenn das Byte ganz links das niedrigstwertige Byte und das Byte ganz rechts das höchstwertige Byte ist, handelt es sich um die Little-Endian-Darstellung des Wortes. Bei geringer Endianness und für das vorherige Wort wird das niedrigstwertige Byte in Zelle Byte 0, das mittlere Byte in Zelle Byte 1 und das höchstwertige Byte in Zelle Byte 2 gespeichert. Dies bedeutet, dass sich in der unteren Speicherzelle ein weniger signifikantes Byte befindet.
Endianness wird nicht für Bits in einem Byte verwendet. Es wird auch nicht für Halbbytes in einem Byte verwendet. Es wird nur für die Bytereihenfolge verwendet.
Der Zahlenstrahl
Eine Zahl ohne Vorzeichen ist eine positive Zahl. Positive Zahlen sind Zahlen von Null nach oben. Es gibt auch negative Zahlen. Auf einem Zahlenstrahl können positive und negative Zahlen dargestellt werden. Der folgende Zahlenstrahl zeigt die positiven und negativen ganzen Zahlen (Ganzzahlen) nahe Null:
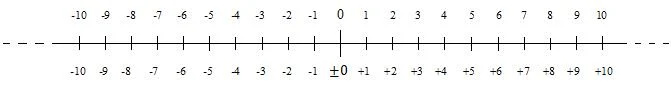
Negative Zahlen nehmen von Null nach unten (nach links) ab. In vielen Situationen wird Null als positiv angesehen. In manchen Situationen wird es jedoch als negativ angesehen. Deshalb steht im Diagramm in der unteren Nummerierung vor der Null ein Plus- und ein Minuszeichen. Wenn eine Zahl positiv ist, kann ihr Vorzeichen weggelassen werden; Dies ist bei der oberen Nummerierung im Diagramm der Fall. Das Minuszeichen vor einer negativen Zahl darf niemals weggelassen werden.
3.2 Addition von Binärzahlen
Im Zusatz:
A + B = S
A heißt Augend, B heißt Summand und S heißt Summe.
Betrachten Sie die folgende Addition zweier positiver Zahlen zur Basis zwei:

In der Basis zwei sind die einzigen möglichen Ziffern 0 und 1. Die Addition in der Basis 2 ähnelt der Addition in der Basis zehn, aber zwei in der Basis zwei ist eins-null (10). Wenn die Summe zweier Bits in einer Spalte 10 beträgt, wird 0 geschrieben und 1 in die unmittelbar linke Spalte übertragen; zur Summe der beiden dortigen Bits addiert werden. Wenn die Gesamtsumme drei beträgt, bedeutet dies 11 in Basis zwei. Die rechte 1 in 11 wird geschrieben und die linke 1 wird übertragen, um zur Summe der unmittelbar linken Spaltenbits addiert zu werden. In beiden Fällen wird die nach links getragene 1 als Übertrag bezeichnet.
Wenn man die vorherige Additionstabelle von rechts liest, gibt es in der zweiten Spalte (von rechts) einen Übertrag, der sich aus 1+1 = 10 ergibt. In der dritten Spalte gibt es einen Übertrag, der sich aus 1+1+ Übertrag von ergibt 1 = 11. In der vierten Spalte gibt es einen Übertrag, der sich aus 0+1+ Übertrag von 1 = 10 ergibt. In der fünften Spalte gibt es keinen Übertrag, da die Summe 0+0+ Übertrag von 1 = 1 ist Der Rest der Spalten beinhaltet keinen Übertrag.
Die Spaltenzählung beginnt am rechten Ende. Bei der 16-Bit-Addition kann es zu einem Übertrag von der achten Spalte zur neunten Spalte (nach links) kommen. Die folgende Tabelle verdeutlicht dies:

Arithmetische und logische Operationen finden im Mikroprozessor auf der Hauptplatine des Computers statt.
Bei einem 8-Bit-Wortcomputer kann der Übertrag nicht automatisch per Hardware vom achten zum neunten Bit wechseln. Um also in einem solchen Computer zwei 16-Bit-Gruppen hinzuzufügen, muss die Addition zweimal in Acht-Acht-Bit-Paaren erfolgen. Der Übertrag wird durch die Software (Programmierung) bewegt und bewirkt.
Um zwei Zahlen zu addieren, können die Zahlen vor der Addition zunächst in die Zweierkomplementform umgewandelt werden (siehe unten).
3.3 Zweierkomplement und seine Subtraktion von Binärzahlen
Auf der Hauptplatine des Computers befinden sich der Speicher, der Mikroprozessor und andere Schaltkreise. Der Speicher besteht aus einer Reihe von Acht-Bit-Zellen. Bei einem Byte geht jedes Bit in eine Zelle. Der Mikroprozessor verfügt über einige Speicherplätze. Diese Speicherorte werden Register genannt. So können im Computer Gruppen von Bytes vorübergehend im Speicher oder in den Registern des Mikroprozessors gespeichert werden.
In jedem dieser Speicher kann jede Zelle entweder eine 1 oder eine 0 annehmen und sonst nichts. Im Leben gibt es positive und negative Zahlen. Eine positive Zahl beginnt mit einem Pluszeichen (+) und eine negative Zahl beginnt mit einem negativen Vorzeichen (-). Wenn das Vorzeichen weggelassen wird, wird die Zahl als positive Zahl betrachtet.
Um dieses Problem der Angabe des Vorzeichens einer Zahl im Computer zu lösen, werden die ganzen Zahlen in Bereichen gespeichert. Ganze Zahlen sind ganze Zahlen. Wenn acht Bits zum Speichern des Bereichs möglicher Zahlen verwendet werden, wird das Bit ganz links als Vorzeichenbit verwendet. Wenn die Zahl mit 0 beginnt, ist die Zahl eine positive Zahl. Wenn sie mit 1 beginnt, ist die Zahl eine negative Zahl. Wenn sechzehn Bits zum Speichern des Bereichs möglicher Zahlen verwendet werden, wird das Bit ganz links als Vorzeichenbit verwendet. Wenn die Zahl mit 0 beginnt, ist die Zahl eine positive Zahl. Wenn sie mit 1 beginnt, ist die Zahl eine negative Zahl. Die Zahlen in dieser Form werden vorzeichenbehaftete Zahlen genannt.
In der Praxis kann es vorzeichenbehaftete Zahlen für 8 Bit, 16 Bit, 32 Bit und 64 Bit geben. Je mehr Bits verwendet werden, desto größer ist der Bereich möglicher Zahlen, die gespeichert werden können.
Zweierkomplement-Ganzzahlen
Beim Zweierkomplement sind die positiven Zahlen die normalen Zählzahlen, mit der Ausnahme, dass die Ziffer ganz links 0 ist. Um die entsprechende negative Zahl für eine bestimmte positive Zahl zu erhalten, invertieren Sie jedes Bit in der Zahl und addieren Sie 1 zum Ergebnis. Die Umkehrung oder das Komplement von 0 ist 1. Die Umkehrung oder das Komplement von 1 ist 0. Die folgenden Tabellen zeigen einige Zweierkomplementzahlen in ihren Bereichen:
| Tabelle 3.31 Zweierkomplement-Ganzzahlen in zwei Bits |
|
|---|---|
| Binär | Dezimal |
| 01 | +1 |
| 00 | +0 |
| elf | -1 |
| 10 | -2 |
Die positiven Binärzahlen sind 00 und 01 (also Null und Eins). Im Bit ganz links zeigt Null an, dass es sich um positive Zahlen handelt. 00 liegt eher in der Mitte des Bereichs. Um -1 zu erhalten, wird festgestellt, dass die Umkehrung der Zahl 01 10 ist. Die Addition von 1 dazu (ganz rechts) ergibt 11.
Da zwei Bits verwendet werden, bleibt nur ein Bit übrig, um die Zahlen im Bereich darzustellen, der aus den Zahlen +1, +0 und -1 besteht, die 01, 00 und 11 entsprechen. Das erste Bit gibt das Vorzeichen an. Es kommt vor, dass 10 für +2 nicht zu diesen drei Binärzahlen gehört. 10 beginnt mit 1, was bedeutet, dass es eine negative Zahl im Zweierkomplement sein muss. Daher ist 10 im Bereich enthalten, was -2 bedeutet.
Mit zwei Bits im Zweierkomplement beträgt die Anzahl aller darstellbaren ganzen Zahlen (positiv und negativ) 2 2 = 4 und nicht 2 2 -1 = 3. Die Nuance ergibt sich aus der Einbeziehung der letzten negativen Zahl, die das Negativ von 2 ist Nummermit – 1. In diesem Fall -2 2-1 = -2 1 = -2. Im Bereich der Zweierkomplementzahlen in 2 Bits gibt es kein +2.
| Tabelle 3.32 Zweierkomplement-Ganzzahlen in vier Bits |
|
|---|---|
| Binär | Dezimal |
| 0111 | +7 |
| 0110 | +6 |
| 0101 | +5 |
| 0100 | +4 |
| 0011 | +3 |
| 0010 | +2 |
| 0001 | +1 |
| 0000 | +0 |
| 1111 | -1 |
| 1110 | 1110 |
| 1101 | -3 |
| 1101 | -3 |
| 1100 | -4 |
| 1011 | -5 |
| 1010 | -6 |
| 1001 | 1001 |
| 1000 | -8 |
Die positiven Binärzahlen reichen von 0000 bis 0111 (also von null bis sieben). Im Bit ganz links zeigt Null an, dass es sich um positive Zahlen handelt. 0000 liegt eher in der Mitte des Bereichs. Um -1 zu erhalten, wird festgestellt, dass der Invertierte der Zahl 0001 1110 ist. Die Addition von 1 dazu (ganz rechts) ergibt 1111. Um -2 zu erhalten, wird der Invertierte von 0010 als 1101 ermittelt. Addiert man dazu 1 ( von ganz rechts) ergibt 1110. Die anderen negativen Binärzahlen wie -3 bis -7 werden auf ähnliche Weise bestimmt.
Da vier Bits verwendet werden, bleiben drei Bits übrig, um die Zahlen im Bereich +7, +6, +5, +4, +3, +2, +1, +0, -1, -2, - darzustellen. 3, -4, -5, -6 und -7 entsprechend 0111, 0110, 0101, 0100, 0011, 0010, 0001, 0000, 1111, 1110, 1101, 1100, 1011, 1010 und 1001.
Der Wert -8, der 1000 entspricht, muss separat adressiert werden. Das erste Bit für alle diese Zahlen gibt das Vorzeichen 0 für positive Zahlen und 1 für negative Zahlen an. Es kommt vor, dass 1000 nicht zu diesen vierzehn Binärzahlen gehört. 1000 beginnt mit 1, was bedeutet, dass es eine negative Zahl sein muss, soweit es das Zweierkomplement betrifft. Daher ist 1000 im Bereich enthalten, was -8 bedeutet.
Mit vier Bits im Zweierkomplement beträgt die Anzahl aller darstellbaren ganzen Zahlen (positiv und negativ) 2 4 = 16 und nicht 2 4 – 1 = 15. Die Nuance ergibt sich aus der Einbeziehung der letzten negativen Zahl, die das Negativ von 2 ist ZahlBreite – 1. In diesem Fall -2 4 -1 = -2 3 = -8. Im Zahlenbereich gibt es kein +8.
Die vorherige Analyse für zwei, vier und breitere Bits im Zweierkomplement kann auf 8 Bit, 16 Bit, 32 Bit und 64 Bit breite Binärzahlen angewendet werden.
Das Zweierkomplement opfert das erste (ganz linke) Bit für das Vorzeichen 0 für eine positive Zahl und 1 für eine negative Zahl. Für die „n“ Bit breite Bitgruppe gibt es 2 N insgesamt positive plus negative Zahlen. Es wären 2 N -1, wäre da nicht die glückliche letzte (kleinste) negative Zahl enthalten. Die höchste positive Zahl ist +2 n-1 -1 und die kleinste negative Zahl ist -2 n-1 -1. Es wäre -2 n-1 -1, wenn da nicht das Glück wäre -2 n-1 inbegriffen.
Subtrahieren von Zahlen im Zweierkomplement
In der Subtraktion:
A – B = D
A heißt Minuend, B heißt Subtrahend und D heißt Differenz.
Um eine positive Binärzahl von einer anderen positiven Binärzahl zu subtrahieren, wird der Minuend im Zweierkomplement geschrieben und der Subtrahend in seinen negativen Zweierkomplementwert umgewandelt. Die mathematische Aussage lautet also:
A+ – B = D
Mit anderen Worten: Bei der Zweierkomplementsubtraktion wird der Subtrahend in eine negative Zahl umgewandelt und dann zum Minuenden addiert.
Beispiel 3.31:
Werten Sie den folgenden Dezimalausdruck im Zweierkomplement mit vier Bits aus:
6 – 4
Lösung:
Die Binärzahl für 6 ist 110. Im 4-Bit-Zweierkomplement ist sie 0110. Die Binärzahl für +4 ist 100. Im 4-Bit-Zweierkomplement ist sie 0100. 0100 muss in eine negative 4 im Zweierkomplement umgewandelt werden Komplement wie folgt: Das Komplement oder die Umkehrung von 0100 ist 1011. Addiert man dazu vom rechten Ende aus 1, wie wir es zusätzlich getan haben, erhält man 1100. Der Dezimalausdruck lautet also:
6 – 4 was wird:
0110 – 0100 also
0110 +(– 0100) = 0110 + 1100 erfolgt wie im vorherigen Additionsabschnitt als:

Hinweis: 0110 +(– 0100) ist dasselbe wie 6 + – 4
Bei der Zweierkomplement-Subtraktion wird jeder Übertrag nach der letzten Spalte nach links in der Addition verworfen. Bei der Dezimalsubtraktion lautet die mathematische Aussage:
6 – 4 = 2
Wenn man das Gleiche im Zweierkomplement macht, ist die Antwort 0010, was +2 im Zweierkomplement-Binärzählen ist. Bei der vorherigen Subtraktion wird eine kleinere Zahl von einer größeren Zahl subtrahiert. Im folgenden Beispiel wird eine größere Zahl von einer kleineren Zahl subtrahiert. Tabelle 3.32 kann herangezogen werden, um zu sehen, ob 0010 wirklich ein Zweierkomplement ist, was äquivalent zu +2 ist.
Beispiel 3.32:
Werten Sie den folgenden Dezimalausdruck im Zweierkomplement mit vier Bits aus:
4 – 6
Lösung:
Die Binärzahl für 4 ist 100. Im 4-Bit-Zweierkomplement ist sie 0100. Die Binärzahl für +6 ist 110. Im 4-Bit-Zweierkomplement ist sie 0110. 0110 muss im Zweierkomplement in eine negative 6 umgewandelt werden wie folgt: Das Komplement oder die Umkehrung von 0110 ist 1001. Addiert man dazu vom rechten Ende aus 1, wie wir es bei der vorherigen Addition getan haben, erhält man 1010. Der Dezimalausdruck lautet also:
4 – 6 was wird:
0100 – 0110 also
0100 +(– 0110) = 0100 + 1010 erfolgt wie im vorherigen Additionsabschnitt als:

Hinweis: 4+ – 6 ist dasselbe wie 0100 +(– 0110).
Bei der Zweierkomplement-Subtraktion wird jeder Übertrag nach der letzten Spalte nach links in der Addition verworfen. Bei der Dezimalsubtraktion lautet die mathematische Aussage:
4 – 6 = -2
Wenn man das Gleiche im Zweierkomplement macht, ist die Antwort 1110, was -2 im Zweierkomplement binärer Zählung ist. Tabelle 3.32 kann herangezogen werden, um zu sehen, ob 1110 wirklich ein Zweierkomplement ist, was für -2 äquivalent ist.
3.4 Multiplikation von Binärzahlen
In der Erklärung:
A x B = P
A heißt Multiplikand, B heißt Multiplikator und P heißt Produkt. Der Ausdruck „A x B“ bedeutet, dass A und B so oft addiert werden, wenn A und B Ganzzahlen (ganze Zahlen) sind.
Die binäre Multiplikation ist dasselbe wie die dezimale Multiplikation. Allerdings geschieht dies nicht im Dezimalformat, sondern im Binärformat. Die Multiplikation des Dezimalausdrucks von 42 x 10 erfolgt binär wie folgt, wobei 42 10 = 101010 2 und 10 10 = 1010 2 :
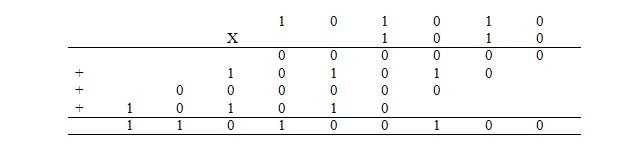
Die 4 addierten Zahlen werden als Teilprodukte bezeichnet. Die Antwort ist das Produkt. Die Addition der Teilprodukte erfolgt auf die gleiche Weise wie zuvor erläutert.
Die Multiplikation kann auch wie folgt gesehen werden: Wenn bei dieser Basis-Zwei-Multiplikation das Bit (Ziffer) im Multiplikator 1 ist, ist das niedrigstwertige Bit seines Teilprodukts das niedrigstwertige Bit des Multiplikanden, der direkt darunter neu eingegeben wird; und die restlichen Bits des Multiplikanden werden nach links wiederholt. Wenn bei dieser Basis-Zwei-Multiplikation das Bit (Ziffer) im Multiplikator 0 ist, besteht sein Teilprodukt aus Nullen mit dem niedrigstwertigen Bit von 0 direkt darunter. Die Anzahl aller Nullen ist die Anzahl der Bits im Multiplikanden.
3.5 Division von Binärzahlen
In der Erklärung:
A ÷ B = Q
A heißt Dividende, B heißt Divisor und P heißt Quotient. Der Quotient kann von einem Rest begleitet werden. Der Ausdruck A ÷ B gibt an, wie oft B addiert werden kann, um A zu ergeben oder nahe daran zu liegen, so dass der Rest 0 oder kleiner als B ist.
Die Teilung kann auf viele Arten erfolgen. Die hier dargestellte Abteilung ist die Restaurierungsabteilung.
Wiederherstellungsabteilung
Dies ist die Methode der langen Division, die in Schulen gelernt wird. Wenn 237 durch 6 geteilt wird, ist das Ergebnis 39, Rest 3. Die 237 10 in Basis 2 ist 11101101 2 und 6 10 in Basis 2 ist 110 2 . Die 39 10 in Basis 2 ist 100111 2 und 3 10 in Basis 2 ist 11 2 .
Also, 11101101 2 dividiert durch 110 2 ergibt 100111 2 Rest 11 2 in Basis zwei. Bei der Wiederherstellungsmethode sind die Binärzahlen gewöhnliche Zahlen und liegen nicht unbedingt im Zweierkomplement vor. Die folgende Struktur unterteilt 11101101 2 um 110 2 um 100111 zu geben 2 Rest 11 2 :

Die Subtraktion erfolgt normalerweise und nicht durch Verwendung des Zweierkomplements. Da dies die Basis zwei ist, ist ein Kredit zwei und nicht zehn. Die Teildividenden betragen 10, 101, 1011, 1010 und 1001. 11 ist der Rest. Da der Divisor dreistellig ist, erfolgt die Division grundsätzlich in Dreiergruppen aus dem gegebenen Dividenden. Der Quotient ist die ganze Zahl (Ganzzahl) und beträgt für dieses Problem 100111. Das Quotienten- und Restergebnis ist wie erwartet.
3.6 Arithmetische Operationen mit Software und Hardware
Das Computer-Motherboard verfügt über eine Uhr. Die Ticken der Uhr werden Impulse genannt. Bei jedem Taktimpuls werden an unterschiedlichen Stellen auf der Hauptplatine eine oder mehrere Entscheidungen getroffen; und das hat mit Programmierung (Software) zu tun.
Im Mikroprozessor gibt es zwei Arten von Schaltkreisen: kombinatorische Logikschaltkreise und sequentielle Logikschaltkreise. Es gibt eine andere Art von Schaltung, die als Multiplexer bezeichnet wird. Addition, Multiplikation und Division können mithilfe der kombinatorischen Logik (Schaltung) innerhalb eines Taktintervalls erfolgen. Während der Programmierung (Software) trifft die Entscheidung bei jedem Taktimpuls mithilfe der sequentiellen Logikschaltungen und Multiplexer.
Bei der Subtraktion im Zweierkomplement sind mindestens zwei Taktimpulse erforderlich. Beim ersten Taktimpuls leitet ein Multiplexer den Subtrahenden zu einer Reihe von NICHT-Gattern (ein NICHT-Gatter pro Ziffer). Beim zweiten Taktimpuls addiert die kombinatorische Logik 1 zum Ausgang der NOT-Gatter und addiert weiterhin den resultierenden Subtrahend und Minuend. Die gesamte Addition kann innerhalb eines Taktintervalls erfolgen.
Addition, Multiplikation und Division können bei der Programmierung mithilfe der Wahrheitstabellen immer noch nicht durchgeführt werden. Dies wird jedoch in diesem Online-Karrierekurs nicht behandelt.
3.7 Logische Operationen im Mikroprozessor
UND, ODER, XOR und Invertieren
UND
Die folgende Tabelle veranschaulicht das bitweise UND. Das bedeutet, dass für zwei verschiedene Binärzahlen die entsprechenden Bits anhand der AND-Wahrheitstabelle UND-verknüpft werden:
Von links nach rechts: 1 UND 1 = 1; 0 UND 1 = 0; 0 UND 0 = 0; 1 UND 0 = 0; und so weiter gemäß der UND-Wahrheitstabelle.
ODER
Die folgende Tabelle veranschaulicht das bitweise ODER. Das bedeutet, dass für zwei verschiedene Binärzahlen die entsprechenden Bits basierend auf der OR-Wahrheitstabelle ODER-verknüpft werden:

Von links nach rechts: 1 ODER 1 = 1; 0 ODER 1 = 1; 0 ODER 0 = 0; 1 ODER 0 = 1; und so weiter gemäß der OR-Wahrheitstabelle.
FREI
Die folgende Tabelle veranschaulicht das bitweise Exklusiv-ODER. Das bedeutet, dass für zwei verschiedene Binärzahlen die entsprechenden Bits basierend auf der XOR-Wahrheitstabelle XOR-verknüpft werden:

Von links nach rechts: 1 XOR 1 = 0; 0 XOR 1 = 1; 0 XOR 0 = 0; 1 XOR 0 = 1; und so weiter gemäß der XOR-Wahrheitstabelle.
Invertieren (NICHT)
Die folgende Tabelle veranschaulicht das bitweise NICHT (Invertieren). Dies bedeutet, dass für eine Binärzahl dieses Mal jedes Bit basierend auf der NOT-Wahrheitstabelle invertiert wird:

Von links nach rechts bewegen, NICHT 1 = 0; NICHT 0 = 1; NICHT 0 = 1; NICHT 1 = 0; und so weiter gemäß der NICHT-Wahrheitstabelle.
Nach rechts oder links verschieben
Nach rechts verschieben
Die folgende Binärzahl wird um 3 Bitpositionen nach rechts verschoben, wobei die Nullen an den frei gewordenen Bitpositionen links eingefügt werden:

Die Verschiebung kann für einen, zwei, drei, vier usw. Plätze erfolgen.
Nach links verschieben
Die folgende Binärzahl wird um 3 Bitpositionen nach links verschoben, wobei die Nullen an den frei gewordenen Bitpositionen rechts eingefügt werden:

Die Verschiebung kann für einen, zwei, drei, vier usw. Plätze erfolgen.
Nach rechts oder links drehen
Das Drehen ähnelt dem Verschieben. Dies geschieht Stück für Stück. Beim Drehen nach rechts fallen die Bits, die das rechte Ende verlassen, nicht ab, wie beim Verschieben; Sie ersetzen nacheinander die frei gewordenen Bits auf der linken Seite. Beim Drehen nach links fallen die Bits, die das linke Ende verlassen, nicht wie beim Verschieben ab; Sie ersetzen nacheinander die frei gewordenen Bits auf der rechten Seite.
Drehe nach rechts
Die folgende Binärzahl wird um 3 Bitpositionen nach rechts gedreht:

Das Drehen kann für eine, zwei, drei, vier usw. Stellen erfolgen.
Nach links drehen
Die folgende Binärzahl wird um 3 Bitpositionen nach links gedreht:

Das Drehen kann für eine, zwei, drei, vier usw. Stellen erfolgen.
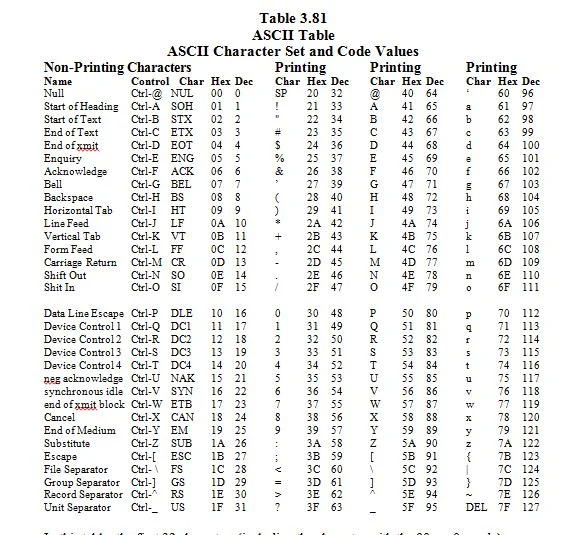
3.8 ASCII-Zeichensatz und seine Codewerte
ASCII steht für „American (U.S.A) Standard Code for Information Interchange“. Stellen Sie sich eine Tastatur mit 96 Tasten vor. Dies ist eine ideale Tastatur, bei der sich die Großbuchstabentasten von den Kleinbuchstabentasten unterscheiden. Jede zweite Taste stellt ein Zeichen dar, das auf einer englischen (USA) Tastatur zu finden ist. Die Zeichen und Codes (entsprechende Nummern für die Zeichen) sind im Folgenden aufgeführt:
In dieser Tabelle sind die ersten 32 Zeichen (einschließlich des Zeichens mit der 00 16 = 0 10 Code) sind nicht druckbare Zeichen. Sie sind Kontrollcharaktere. Sie sind nicht auf dem Bildschirm (Monitor) zu sehen, wo alles gleich ist. Sie haben nur Auswirkungen. Lassen Sie uns später mehr darüber besprechen.
Die restlichen Zeichen sind Druckzeichen; Sie sind auf dem Bildschirm zu sehen. Es gibt 128 ASCII-Zeichen. 2 7 = 128. 1.111.111 2 = 127 10 . Die 7 in 2 7 bedeutet 7 Bit.
Jetzt 1111111 2 + 1 2 ist das gleiche wie:
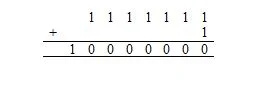
Hier 10.000.000 2 = 128 10 . Es sind 128 10 Zeichen in der vorherigen Liste (Tabelle) der ASCII-Zeichen. Dazu gehört auch das Nullzeichen, dessen Code zur Basis sechzehn (hexadezimal) 00 ist, was 0 zur Basis zehn entspricht.
Da es insgesamt 128 Zeichen gibt, ergeben 128 minus 32 nicht druckbare Zeichen 96 druckbare Zeichen. In diesem Abschnitt wird davon ausgegangen, dass es eine ideale Tastatur mit 96 Zeichen gibt, bei denen es sich um druckbare Zeichen handelt. Auf dieser idealen Tastatur unterscheiden sich die Tasten für die englischen Großbuchstaben von den Tasten für die englischen Kleinbuchstaben.
Jedes Zeichen auf der Tastatur wird durch eine Basis-Zwei-Zahl von 7 Bits dargestellt, die nicht in der Liste angezeigt werden. Der Großbuchstabe „N“ wird beispielsweise durch die sieben Bits 1001110 zur Basis 2 dargestellt. Um 1001110 umzuwandeln 2 zur Basis 16, stellen Sie ihm eine 0 voran und gruppieren Sie das Ergebnis wie folgt in Vier-Bit-Untergruppen:
| 0100 | 1110 | 2 = | 4 | E | 16
Das ist 01001110 2 = 4E 16 . Um 4E zu konvertieren 16 Gehen Sie zur Basis zehn wie folgt vor:
4 x (16) 1 + E x (16) 0 = 4 x 16 + E x 1 = 4 x 16 + 14 x 1 = 64 + 14 = 78 10
Rechts von „N“ in der Liste (Tabelle) steht die Hexadezimalzahl 4E und die Dezimalzahl 78.
Als weiteres Beispiel wird das Zeichen „[“ durch die sieben Bits 1011011 in Basis 2 dargestellt. Um 1011011 umzuwandeln 2 zur Basis 16, stellen Sie ihm eine 0 voran und gruppieren Sie das Ergebnis wie folgt in Vier-Bit-Untergruppen:
| 0101 | 1011 | 2 = | 5 | B | 16
Das ist 01011011 2 = 5B 16 . Gehen Sie wie folgt vor, um 5B16 in die Basis Zehn umzuwandeln:
5 x (16) 1 + B x (16) 0 = 5 x 16 + B x 1 = 5 x 16 + 11 x 1 = 80 + 11 = 91 10
Rechts von „[“ in der Liste (Tabelle) steht die Hexadezimalzahl 5B und die Dezimalzahl 91.
Als weiteres Beispiel wird das Zeichen für die Dezimalzahl „5“ durch die sieben Bits 0110101 in Basis 2 und dargestellt nicht 0000101 in Basis 2. Um 0110101 umzuwandeln 2 zur Basis 16, stellen Sie ihm eine 0 voran und gruppieren Sie das Ergebnis wie folgt in Vier-Bit-Untergruppen:
| 0011 | 0101 | 2 = | 5 | B | 16
Das ist 00110101 2 = 35 16 . Um 3516 in Basis zehn umzuwandeln, gehen Sie wie folgt vor:
3 x (16) 1 + 5 x (16) 0 = 3 x 16 + 5 x 1 = 3 x 16 + 5 x 1 = 48 + 5 = 53 10
Rechts von „5“ in der Liste (Tabelle) steht die Hexadezimalzahl 35 und die Dezimalzahl 53.
Da der Computer in Bytes arbeitet, werden beim Drücken einer Taste auf der idealen Tastatur acht Bits an den Mikroprozessor (Hauptplatine) gesendet. Die ideale Tastatur ist ein Peripheriegerät, das von der Systemeinheit (Basiseinheit) des Computers getrennt ist. Es verfügt über einen elektronischen Schaltkreis (IC), der die sieben Bits erzeugt und ihnen eine Null voranstellt, bevor sie sie über ihr Kabel an die Hauptplatine der Systemeinheit sendet. Vom Eingangsport (Eingangsschaltkreis) des Motherboards gelangt es zum Mikroprozessor, der sich ebenfalls auf dem Motherboard befindet. Vom Mikroprozessor gelangt es zum Speicher, der ebenfalls auf der Hauptplatine verbaut ist.
Wenn also die „N“-Taste auf der idealen Tastatur gedrückt wird, werden acht Bits 01001110 an den Mikroprozessor übertragen. Vom Mikroprozessor werden sie in den Speicher übernommen, wo sie als Byte an einem Speicherort verbleiben. Der Computerprogrammierer sollte bedenken, dass die acht Bits von 01001110 2 ist das gleiche wie 4E 16 Das ist dasselbe wie 78 10 .
Wenn die „[“-Taste auf der idealen Tastatur gedrückt wird, werden acht Bits 01011011 zum Mikroprozessor übertragen. Vom Mikroprozessor werden sie in den Speicher übernommen, wo sie als Byte an einem Speicherort verbleiben. Der Computerprogrammierer sollte bedenken, dass die acht Bits von 01011011 2 ist das gleiche wie 5B 16 Das ist dasselbe wie 91 10 .
Wenn die Taste „5“ auf der idealen Tastatur gedrückt wird, werden acht Bits 00110101 als Zeichen und nicht als Dezimalzahl an den Mikroprozessor übertragen. Vom Mikroprozessor werden sie in den Speicher übernommen, wo sie als Byte an einem Speicherort verbleiben. Der Computerprogrammierer sollte bedenken, dass die acht Bits von 00110101 2 ist das gleiche wie 35 16 Das ist dasselbe wie 5310 10 .
Es gibt Zeiten, in denen ein Programm ausgeführt wird und darauf wartet, dass die Dezimalzahl 5 in den Computer eingegeben wird. Wenn in dieser Situation die Taste „5“ auf der idealen Tastatur gedrückt wird, wird immer noch der Acht-Bit-Code 00110101 an den Mikroprozessor übertragen. Da die Dezimalzahl 5 und nicht das Zeichen „5“ benötigt wird, verwendet ein Codestück (Kurzprogramm) aus dem Speicher den Mikroprozessor, um den Zeichencode 00110101 zur Basis zwei in die Zweierkomplementzahl 00000101 umzuwandeln 2 bevor es als Zweierkomplement-Byte an einen Speicherort gesendet wird. Der Computerprogrammierer muss bedenken, dass 00000101 5 bedeutet 10 in Basis 2 und unterscheidet sich von den Codenummern 00110101 2 , 35 16 und 53 10 was das Zeichen „5“ bedeutet. Um die Zweierkomplementzahl 00000101 im Speicher anzuzeigen, muss ein weiteres kurzes Programm 00000101 aus dem Speicher in 00110101 konvertieren. Es ist 00110101, was dasselbe wie 35 ist 16 Das ist dasselbe wie 53 10 das auf dem Monitor angezeigt (oder vom Drucker auf Papier gedruckt) wird.
3.9 Gleitkommazahlenformat
Eine Zahl ohne Dezimalteil ist eine ganze Zahl. Die Zahl 36 ist eine ganze Zahl. 36,375 ist keine ganze Zahl. Es handelt sich um eine Dezimalzahl mit einem Dezimalteil. Der Dezimalteil von .375 ist ein Bruch, der kleiner als 1 ist.
36,375 wird in Dezimalform interpretiert als:
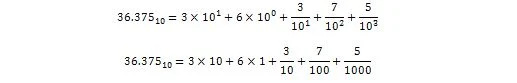
Jetzt:
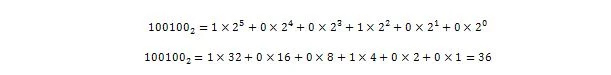
Also 100100 2 = 3610, was der ganzzahlige Teil von 36,375 ist 10 .
Jetzt:
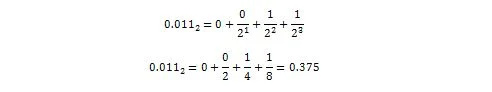
Also 0,011 2 = 0,375 10 Das ist der Dezimalzahlteil von 36,375 10 .
∴ 36.375 10 = 100100,011 2
Anders ausgedrückt:
100100.011 2 = 36.375 10
Zahlen werden im Computer zur Basis 2 und nicht zur Basis 10 dargestellt, wobei alles gleich ist. Da eine Zelle in einem Register im Mikroprozessor oder eine Zelle im Speicher nur 1 oder 0 annehmen kann, gibt es keinen Platz zum Speichern eines Dezimalpunkts. Dies stellt ein Problem dar. Als Auflösung gibt es die IEEE-754 Single Precision 32-Bit-Gleitkommadarstellung und die IEEE-754 Double Precision 64-Bit-Gleitkommadarstellung.
32-Bit-Gleitkommazahlenformat
Die Zahl 100100.0112 kann ausgedrückt werden als:
100100.011 2 = 1,00100011 2 x 2 +5
Die rechte Seite des =-Symbols wird in der Mathematik als Basis-Zwei-Standardform der linken Seite von 100100,011 bezeichnet 2 .
Jetzt 00100011 von 1,00100011 2 auf der rechten Seite des =-Symbols, ohne die vorangehende „1“. und ohne die 2 für die Basis wird der explizite Signifikand genannt. In diesem Fall wird der Binärpunkt um fünf Stellen nach links verschoben, um die „1“ zu erhalten. Verwechseln Sie nicht Dezimalpunkt und Binärpunkt. Der Binärpunkt steht für die Basis 2, während der Dezimalpunkt für die Basis 10 steht. Die „1“. gefolgt von 00100011 auf der rechten Seite des =-Symbols, ohne die 2 für die Basis, bildet den wahren Signifikanten. Allerdings wird 1,00100011 als impliziter Signifikand bezeichnet.
Nach dem Signifikanten auf der rechten Seite steht „x 2“. +5 ' Ausdruck. Bei diesem Ausdruck wird +5 als Exponent bezeichnet. Das Pluszeichen bedeutet, dass der Binärpunkt um fünf Stellen nach vorne verschoben werden muss, um an seiner normalen ursprünglichen Position zu sein, und 2 ist die Basis für die Nummerierung. Die vorherige Gleichung kann umgekehrt geschrieben werden als:
1.00100011 2 x 2 +5 = 100100,011 2
Bei der 32-Bit-Gleitkommadarstellung ist es „1.00100011 2 x 2 +5 ” das verwendet wird und nicht nur „100100.011 2 “. Die 2 für die Basis ist nicht verzeichnet. Die 32-Bit-Gleitkommadarstellung für „1.00100011 2 x 2 +5 ” Zahl, die 36,375 entspricht 10 = 100100,011 2 ist in der folgenden Tabelle dargestellt:

Es gibt 32-Bit-Positionen, die vom rechten Ende beginnend bei 0 nummeriert werden. Das erste Bit am linken Ende ist das Vorzeichenbit. Wenn die Zahl positiv ist, ist dieses Bit 0. Wenn die Zahl negativ ist, ist dieses Bit 1 (-1 besteht aus zwei Zeichen und kann nicht in eine Zelle eingefügt werden). Die 1.00100011 2 x 2 +5 was 36,375 entspricht 10 was ebenfalls 100100,011 entspricht 2 ist eine positive Zahl. Das erste Bit ist also 0.
Es gibt acht Bitpositionen für den Exponenten, beginnend von Position 30 bis einschließlich Position 23. Der dort geschriebene Exponent ist jedoch 10000100 2 was gleich 132 ist 10 . Der Exponent der interessierenden Zahl ist tatsächlich +5 der Basis zwei. Was passiert also?
Im 32-Bit-Format wird ein Exponent von 0 nun als 01111111 geschrieben 2 was gleich 127 ist 10 . Die +5 10 ist +101 2 . Also, wenn ich bei 10000100 ankomme 2 im Exponententeil der Tabelle 101 2 wurde zu 01111111 hinzugefügt 2 , entsprechend. Das bedeutet, dass 5 zu 127 addiert wurde, um 132 zu erhalten 10 .
Der Signifikand ohne „1.“ verringerte die Positionen 22 auf einschließlich 15. Beachten Sie, dass die 1 von „1.“ wurde im 32-Bit-String nicht angegeben. Es wird nie angezeigt – akzeptieren Sie das. Die restlichen Zellen bis zur Position 0 werden mit Nullen gefüllt.
Wenn der tatsächliche Exponent -5 ist, wird 5 von 127 subtrahiert 10 122 haben 10 . Dies entspricht der Subtraktion von 101 2 von 01111111 2 01111010 haben 2 .
Bei allen vorherigen Abbildungen ist die Zahl +1 gleich 1,0 x 2 0 = 1,0 x 1 = 1,0 wird dargestellt als:

Beachten Sie, dass die „1.“ von 1,0 x 2 0 ist im Format nicht angegeben. Es wird nie angegeben. Der nächste gemischte Bruch, der nach 1,0 positiv verläuft, ist:

Beachten Sie die 1 am rechten Ende. Diese Darstellung ist die Zahl:

Der Unterschied zwischen 1,0000001192092896 und 1,0 ist:
1,0000001192092896 – 1,0 = 0,0000001192092896
Die Zahlen mit Dezimalteilen sind gemischte Brüche. Nicht alle Brüche zwischen 1 10 und 2 10 im Computer dargestellt werden kann. Es kann davon ausgegangen werden, dass die kleinste Bruchlücke zwischen den aufeinanderfolgenden gemischten Zahlen im 32-Bit-Gleitkommaformat 0,0000001192092896 beträgt. Erwarten Sie, dass das Intervall für die doppelte Genauigkeit kleiner ist. Beachten Sie die folgende Abbildung.
Bei der Darstellung der Zahl folgt 0,0 nicht den vorherigen Argumenten. Die Darstellung für 0.0 ist deklariert und muss als solche gelernt werden. Um 0,0 darzustellen, sind alle Zellen für den Signifikanten 0 und alle Zellen für den Exponenten sind ebenfalls Null. Das Vorzeichenbit kann 0 oder 1 sein. Leider führt dies zu positiven 0 und negativen 0 wie folgt:

Im wirklichen Leben gibt es nur eine Null. Positive 0 und negative 0 existieren nicht. Allerdings wird 0 normalerweise als positiv angesehen. Aufgrund dieser speziellen Formatbeschreibung gibt es hier positive 0 und negative 0. Der Zahlenstrahl (siehe oben) kann auch +0 und -0 haben, es existiert jedoch nur eine Null.
64-Bit-Gleitkommazahlenformat
Das 64-Bit-Gleitkommaformat ähnelt dem 32-Bit-Format, weist jedoch folgende Unterschiede auf:
- Es gibt 64 Bits zur Darstellung einer Zahl.
- Nach dem Vorzeichenbit folgen 11 Bits für die Exponentenzahl.
- Die Exponentenzahl für den Nullindex (2 0 ) ist 1023 10 = 01111111111 2 .
- Auf die elf Bits folgen 52 Bits für den expliziten Signifikanten.
- Es verfügt über einen größeren Zahlenbereich als das 32-Bit-Format.
Beachten Sie, dass die „1.“ das am Anfang des Signifikanten steht, ist immer noch nicht in den 64 Bits enthalten, ebenso wie es nicht in den 32 Bits für das 32-Bit-Format enthalten ist.
Einer der wichtigsten Unterschiede zwischen dem 64-Bit-Format und dem 32-Bit-Format besteht darin, dass der Unterschied zwischen den aufeinanderfolgenden gemischten Brüchen im 64-Bit-Format kleiner ist als der im 32-Bit-Format.
Im 64-Bit-Format kann das Intervall (Lücke) zwischen 1,0 und dem nächsten gemischten Bruch wie folgt berechnet werden:
1,0 ist
0 01111111111 00000000000000000000 00000000000 000000000000000000000 2
Dies entspricht der „1“, die in der Zeichenfolge nicht angegeben wurde, multipliziert mit 2 hoch (Index) 0 (wobei der Exponent 1023 ist). 10 = 01111111111 2 für 2 0 = 1). Die Zeichenfolge ist 1,0 x 2 0 .
Der nächste gemischte Bruch größer als 1,0 ist:
0 01111111111 00000000000000000000 00000000000 000000000000000000001 2
Dies entspricht „1“. was in der Zeichenfolge nicht angegeben ist, gefolgt von 51 Nullen und dann 1, multipliziert mit 2 hoch 0 (wobei der Exponent 1023 ist). 10 = 011111111112 2 für 2 0 = 1). Das ist dasselbe wie:
+2 0 × (1 + 2− -52 ) ≈ 1,0000000000000002
Das ≈ bedeutet ungefähr gleich.
Jetzt:
1,0000000000000002 – 1,0 ≈ 0,0000000000000002
Der entsprechende Intervallwert für ein 32-Bit-Format ist 0,0000001192092896 ≈ 0,00000012.
0,0000000000000002 ist viel kleiner als 0,00000012. Es gibt also weitaus mehr gemischte Brüche zwischen zwei aufeinanderfolgenden ganzen Zahlen (z. B. 3 und 4) im 64-Bit-Format als zwischen zwei aufeinanderfolgenden ganzen Zahlen im 32-Bit-Format.
Die Anzahl der gemischten Brüche zwischen zwei aufeinanderfolgenden ganzen Zahlen auf der Zahlengeraden ist unendlich. Daher kann kein Format (z. B. 32-Bit oder 64-Bit) alle gemischten Brüche zwischen zwei aufeinanderfolgenden ganzen Zahlen (ganzen Zahlen) bereitstellen. Je kleiner die Lücke (Intervall) zwischen zwei aufeinanderfolgenden ganzen Zahlen ist, die durch ein Format (z. B. 32-Bit oder 64-Bit) bereitgestellt wird, desto größer ist die Anzahl der gemischten Brüche zwischen den aufeinanderfolgenden ganzen Zahlen (für den Zahlenstrahl).
Die Gründe dafür, dass das 64-Bit-Format im Vergleich zum 32-Bit-Format als doppelte oder höhere Genauigkeit beschrieben wird, liegen darin, dass das Intervall zwischen zwei aufeinanderfolgenden gemischten Brüchen, die durch zwei aufeinanderfolgende ganze Zahlen begrenzt werden, beim 64-Bit-Format kleiner ist als die entsprechenden 32 -Bit-Formatintervall. Außerdem gibt es für das 64-Bit-Format mehr mögliche gemischte Brüche zwischen zwei begrenzten ganzen Zahlen als entsprechend für das 32-Bit-Format.
Konvertieren eines Dezimalteils (Bruch) einer Dezimalzahl in einen Binärteil
Die 36,375 ist eine Dezimalzahl mit dem Dezimalteil „.375“. Der Dezimalteil von „.375“ ist ein Bruch zwischen null und eins. Die 0,5 in der Basis zehn hat den gleichen Wert wie 1/2 in der Basis zwei. Die 0,5 10 Das wird mit der Basis-Zwei-Erweiterung ausgedrückt:
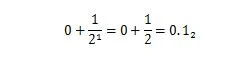
Es ist nicht 0,101 2 was 0,625 bedeutet 10 . Der Dezimalteil einer Dezimalzahl hat seinen entsprechenden Binärteil für die entsprechende Binärzahl. Um also eine Dezimalzahl wie 36,375 umzuwandeln 10 Zur Basis zwei konvertieren Sie 36 in eine Binärdatei und dann .375 ebenfalls in eine Binärdatei. Verbinden Sie dann beide Ergebnisse mit dem Binärpunkt. Die Methoden zum Konvertieren der beiden Abschnitte sind unterschiedlich. Wie man eine dezimale Ganzzahl in die Basis 2 umwandelt, wird in Kapitel 1 erklärt.
Um den Dezimalbruch in einen Binärbruch umzuwandeln, führen Sie die folgenden Schritte aus:
- Multiplizieren Sie den Dezimalbruch (Dezimalteil) mit 2. Die daraus resultierende ganze Zahl ist die erste Binärziffer.
- Wiederholen Sie den vorherigen Schritt mit dem gebrochenen Dezimalergebnis, um die nächste Binärziffer zu erhalten.
- Wiederholen Sie den vorherigen Schritt so lange, bis das Dezimalbruchergebnis .0000- beträgt.
Beispiel: Konvertieren Sie den Bruchteil von 36,375 10 zum entsprechenden Bruchteil in Basis zwei.
Lösung:
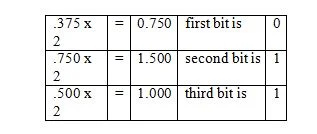
Beachten Sie, dass im dritten Schritt .500 mit 2 multipliziert wurde und nicht 1.500. Der binäre entsprechende Bruch wird in der letzten Spalte von oben gelesen. Somit ergibt sich folgendes Ergebnis:
.375 10 = .011 2
Konvertieren eines Binärteils (Bruch) einer Binärzahl in einen Dezimalteil
Um dies zu erreichen, entwickeln Sie den binären Bruch in reziproken Potenzen von 2.
Beispiel: Konvertieren Sie den Bruchteil von 100100,011 2 zum entsprechenden Bruchteil zur Basis zehn.
Lösung:
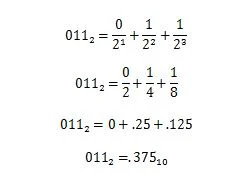
3.10 Zahlenpräfixe in der Informatik
Im normalen Leben bedeutet 1 Kilo 1000, was in k (Kleinbuchstaben) wie 1 kg abgekürzt wird. In der Informatik bedeutet 1 Kilo 2 10 = 1024, wird jedoch in K (Großbuchstaben) abgekürzt, wie in 1Kbits. Im normalen Leben bedeutet 1 Mega 1.000.000, was in M (Großbuchstaben) wie 1Mg abgekürzt wird. In der Informatik bedeutet 1 Mega 2 zwanzig = 1.048.576 = 2 10 x 2 10 = 1024 x 1024 = 1.048.576 und wird immer noch in M (Großbuchstaben) wie bei 1 Mbit abgekürzt. Im normalen Leben bedeutet 1 Giga 1.000.000.000 und wird in G (Großbuchstaben) wie 1Gg abgekürzt. In der Informatik bedeutet 1 Giga 2 30 = 1.073.741.824 = 2 10 x 2 10 x 2 10 = 1024 x 1024 x 1024 = 1.073.741.824 und wird immer noch in G (Großbuchstaben) abgekürzt, wie in 1Gbits. Die folgende Tabelle gibt die Bedeutung von vier Präfixen im normalen Leben und in der Informatik an:
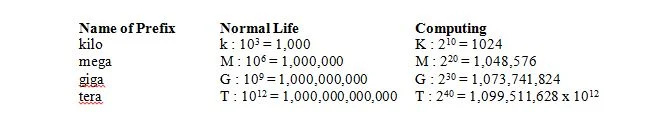
3.11 Probleme
Dem Leser wird empfohlen, alle Probleme in einem Kapitel zu lösen, bevor er mit dem nächsten Kapitel fortfährt.
- Zeichnen Sie einen Zahlenstrahl mit ganzen Zahlen von -10 bis +10.
- Addieren Sie die folgenden Binärzahlen im 8-Bit-Zweierkomplement: 101010 2 und 1111 2 .
- Verwenden Sie nur den Zweierkomplement-Ansatz in 8 Bit, um die Binärzahl 1111 zu subtrahieren 2 aus der Binärzahl 101010 2 .
- Finden Sie das Produkt von 10110 2 x 1101 2 in Basis zwei.
- Teilen Sie 36.375 10 um 1000 10 im Dezimal- und im Binärformat und vergleichen Sie die Ergebnisse.
- Verwenden Sie die 8 Bits Ihrer Wahl, um das logische AND, OR, XOR, Invertieren, Shift Right, Shift Left, Rotate Right und Rotate Left zu veranschaulichen. Jedes Byte sollte eine Mischung aus Einsen und Nullen haben.
- a) Schreiben Sie den numerischen Code für das ASCII-Zeichen Null im Hexadezimal-, Binär- und Dezimalformat.
b) Schreiben Sie den numerischen Code für das ASCII-Zeichen „1“ im Hexadezimal-, Binär- und Dezimalformat.
c) Schreiben Sie den numerischen Code für das ASCII-Zeichen „A“ im Hexadezimal-, Binär- und Dezimalformat.
d) Schreiben Sie den numerischen Code für das ASCII-Zeichen „a“ im Hexadezimal-, Binär- und Dezimalformat. - Konvertieren Sie 49,49 10 in Basis zwei. Konvertieren Sie Ihr Ergebnis in das IEEE 32-Bit-Gleitkommaformat.
- a) Wie unterscheidet sich das IEEE 64-Bit-Gleitkommaformat vom 32-Bit-Format?
b) Geben Sie die beiden verwandten Gründe an, warum das 64-Bit-Format als doppelte oder höhere Genauigkeit gegenüber dem beschrieben wird
32-Bit-Format.