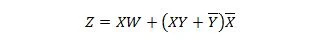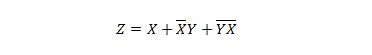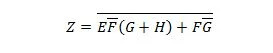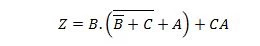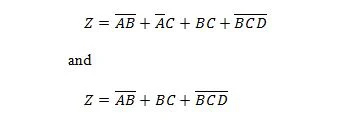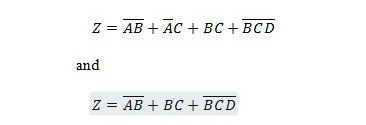Kapitel 2: Boolesche Algebra und ihre zugehörigen Computerkomponenten

Kapitel 2: Boolesche Algebra und ihre zugehörigen Computerkomponenten

2.1 Grundlegende boolesche Operatoren

Gehen Sie davon aus, dass ich (der Autor) groß bin und Sie (der Leser) groß sind. Wenn Sie jemand fragt, ob wir beide groß sind, würden Sie „Ja“ (wahr) sagen. Wenn er fragt, ob wir beide klein sind, würden Sie „Nein“ sagen (falsch). Wenn Sie klein und ich groß sind und er Sie fragt, ob Sie oder ich groß sind, wäre Ihre Antwort „Ja“ (wahr). Wenn er fragt, ob Sie und ich beide groß sind, hätten Sie keine Antwort. Sie könnten weiter sagen, dass die letzte Frage nicht gestellt werden sollte oder dass es auf die Frage keine Antwort gibt. Nun, ich möchte, dass Sie (der Leser) wissen, dass diese Frage heute unter bestimmten Umständen gestellt werden sollte.

In der Biologie ist ein Mensch entweder groß oder klein. Es sind die „Umweltbedingungen“, die dazu führen, dass die Person eine mittlere Körpergröße hat. Ein Wissenschaftler, George Boole, hat eine Reihe von Antworten oder Regeln für diese Art von Fragen definiert. Diese Regeln erfahren Sie in diesem Abschnitt des Online-Karrierekurses (Kapitel). Diese Regeln werden heute in den Bereichen Informatik, Programmierung, Elektronik und Telekommunikation verwendet. Tatsächlich gäbe es ohne diese Regeln keinen Computer, wie er heute üblich ist; Sie hätten nicht auch die Programmierung, wie sie heute üblich ist.

Richtig oder falsch
Eine einfache Aussage in menschlicher Sprache ist an sich entweder wahr oder falsch. Wenn ich sage: „Ich bin groß“, ist das entweder wahr oder falsch. Wenn ich sage: „Du bist groß“, ist das entweder wahr oder falsch. Wenn ich groß und Sie klein bin und die Frage gestellt wird, ob sowohl Sie als auch ich groß sind, muss in der Booleschen Logik eine Antwort mit wahr oder falsch gegeben werden. Welches dieser beiden sollte gegeben werden? Boole hat diese Frage nicht wirklich beantwortet. Er hat einfach eine Reihe von Regeln aufgestellt, die wir befolgen sollten. Die gute Nachricht ist, dass es keine Unklarheiten gibt, wenn Sie diese Regeln im richtigen Kontext befolgen. Dank dieser Regeln haben wir heute Computer und Programmierung. Die Regeln werden Ihnen jetzt gegeben. Die Regeln können nicht wirklich erklärt werden; du akzeptierst sie einfach. Die Regeln sind in drei Überschriften unterteilt: UND, ODER und NICHT.

UND
Die Frage kann gestellt werden, wenn sowohl Sie als auch ich groß sind. Meine Größe und Ihre Größe werden dann durch das UND-Regelwerk kombiniert. Dies sind die UND-Regeln, die es zu befolgen gilt:

false AND false = false
falsch UND wahr = falsch
wahr UND falsch = falsch
wahr UND wahr = wahr

Nun, groß sei wahr und klein sei falsch. Das heißt, wenn ich klein bin UND du klein bist, dann bist du und ich klein. Wenn ich klein bin UND du groß bist, dann bist du und ich klein; Das ist die boolesche Antwort, die Sie akzeptieren müssen. Wenn ich groß bin UND du klein, dann bist du und ich beide klein. Wenn ich groß bin UND du groß bist, dann sind du und ich groß. All dies sind UND-Boolesche Regeln, die Sie (der Leser) einfach akzeptieren müssen.

ODER
Die Frage kann gestellt werden, wenn Sie ODER ich groß sind. Meine Größe und Ihre Größe werden dann durch das ODER-Regelwerk kombiniert. Dies sind die OR-Regeln, die Sie befolgen sollten:

false OR false = false
falsch ODER wahr = wahr
wahr ODER falsch = wahr
wahr ODER wahr = wahr

Auch hier gilt: Groß sei wahr und Klein sei falsch. Das heißt, wenn ich klein bin ODER du klein bist, dann bist du ODER ich klein. Wenn ich klein bin ODER du groß bist, dann bist du oder ich groß. Wenn ich groß bin ODER du klein bist, dann bist du ODER ich groß. Wenn ich groß bin ODER du groß bist, dann bist du oder ich groß. All dies sind boolesche Regeln, die Sie akzeptieren müssen.

NICHT
Nun gibt es in der Booleschen Logik nur zwei Zustände (mögliche Antworten). Das heißt, wenn Sie NICHT groß sind, sind Sie klein. Wenn Sie NICHT klein sind, sind Sie groß; nichts anderes. Dies sind die NICHT-Regeln, die es zu befolgen gilt:

NICHT falsch = wahr
NICHT wahr = falsch

Gehen Sie davon aus, dass Sie eine Schnur (oder Feder) haben, die Sie verlängern (ziehen) können. Während sich die Zeichenfolge in ihrem natürlichen Zustand befindet, würden Sie sie verlängern, wenn ich „NICHT kurz“ sage. das ist die Interpretation. Während die Saite gedehnt ist und ich „NICHT lang“ sage, würden Sie zulassen, dass sie sich zusammenzieht; das ist die Interpretation.

Sie müssen sich alle vorgegebenen Regeln in ihren verschiedenen Kategorien merken.

Mehr als zwei Operanden
In einer Computersprache werden AND, OR und NOT jeweils als Operatoren bezeichnet. Für den NOT-Operator benötigen Sie nur einen Operanden (Wert für einen Operator), um eine Antwort zu erhalten. Für die AND- oder OR-Operatoren können Sie mehr als zwei Operanden verwenden. Die vorherigen Fälle zeigen zwei Operanden für AND und OR. Sie können drei Operanden für AND wie folgt verwenden:

false AND false AND false = false
falsch UND falsch UND wahr = falsch

Das sind zwei Zeilen; Jeder hat zwei UND-Operatoren. Bei drei Operanden sind es tatsächlich neun Zeilen. Beim AND-Operator ist nur die letzte Zeile (neunte Zeile) gleich true; Alle vorhergehenden Zeilen sind falsch. Beachten Sie, dass bei zwei Operanden für AND immer noch nur die letzte Zeile wahr ist; Alle vorangehenden drei Zeilen sind falsch. Wenn es vier Operanden gibt, gibt es 16 Zeilen und nur die letzte Zeile ist für den UND-Operator wahr.

Das Muster für AND und das Muster für OR sind unterschiedlich. Bei drei Operanden für zwei OR-Operatoren gibt es auch neun Zeilen und nur die erste Zeile ist dieses Mal falsch. Die zweite bis neunte Zeile ist wahr. Beachten Sie, dass bei zwei Operanden für OR immer noch nur die erste Zeile wahr ist; alle verbleibenden drei Zeilen sind falsch. Wenn die Operanden für OR vier sind, gibt es auch 16 Zeilen.

Der NOT-Operator behandelt nur einen Operanden. Das NICHT-falsche ist wahr und das NICHT-wahre ist falsch.

2.2 Zwei-Operanden-Wahrheitstabelle und ihre elektronischen Komponenten

In der Mathematik gibt es ein Thema namens Algebra. Ein kleiner Teil davon wurde im vorherigen Kapitel gesehen. Es gibt eine Art Algebra namens Boolesche Algebra. In der Booleschen Algebra wird „wahr“ durch die Basis-zwei-Ziffer identifiziert, die 1 ist, und falsch wird durch die Basis-zwei-Ziffer identifiziert, die 0 ist.

Bei den internen Komponenten der Rechnereinheit handelt es sich um elektronische Bauteile. Die Systemeinheit des Computersystems weist digitale elektronische Komponenten auf. Die UND-Verknüpfung erfolgt durch eine kleine elektronische Komponente, das sogenannte UND-Gatter. Die ODER-Verknüpfung erfolgt durch die kleine elektronische Komponente, das sogenannte ODER-Gatter. Die NICHT-Operation wird von der kleinen elektronischen Komponente namens NOT-Gatter durchgeführt. Zu viele dieser Gatter können sich in einem IC-Chip (Integrated Circuit) befinden.

UND Wahrheitstabelle und ihr Tor
Die folgende Tabelle gibt die UND-Wahrheitstabelle und ihr Symbol für das UND-Gatter (kleiner Schaltkreis) an:

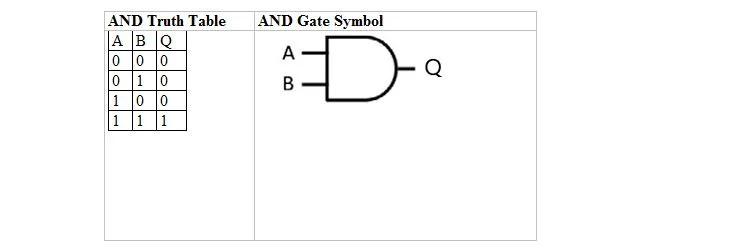
Sowohl für die UND-Wahrheitstabelle als auch für ihr Gatter sind A und B zwei Eingangsvariablen. Q ist die Ausgangsvariable. A ist entweder 1 oder 0. B ist entweder 1 oder 0. Q ist entweder 1 oder 0. Die UND-Wahrheitstabelle mit Einsen und Nullen ist dieselbe wie das vorherige Wahr/Falsch-UND-Wahrheitslayout (Tabelle). Die UND-Gleichung lautet:

A . B = Q

wobei der Punkt (.) UND (boolesch) bedeutet. Der Punkt kann weggelassen werden, um AB = Q zu erhalten, was dasselbe bedeutet (UND).

Hinweis: Die Bits für A und B in den vier Zeilen sind als Paare die ersten vier Zahlen in der Basis zwei, beginnend bei 0 (oder 00), d. h. 00, 01, 10, 11.

Die folgende Tabelle enthält die OR-Wahrheitstabelle und ihr OR-Gatter-Symbol (kleiner Schaltkreis):

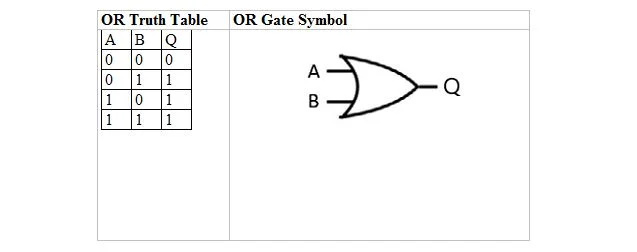
Sowohl für die OR-Wahrheitstabelle als auch für ihr Gatter sind A und B zwei Eingabevariablen. Q ist die Ausgangsvariable. Die ODER-Wahrheitstabelle mit Einsen und Nullen ist dieselbe wie das vorherige Wahr/Falsch-ODER-Wahrheitslayout (Tabelle).

Die OR-Gleichung lautet:

A + B = Q

Wobei das + hier ein boolesches ODER bedeutet und nicht eine Addition. Die Gleichung wird als „A oder B gleich Q“ gelesen.

Die folgende Tabelle enthält die NOT-Wahrheitstabelle und ihr NOT-Gatter-Symbol (kleiner Schaltkreis):

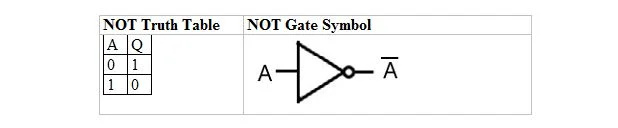
Die NOT-Wahrheitstabelle oder das NOT-Gatter hat nur einen Eingang und einen Ausgang. Wenn der Eingang 0 ist, ist der Ausgang 1. Wenn der Eingang 1 ist, ist der Ausgang 0. Das NOT-Gatter führt eine Art Invertierung durch. Die Ausgabevariable ist dieselbe wie die Eingabevariable, jedoch mit einem Balken (überstrichen). Die NICHT-Wahrheitstabelle mit Einsen und Nullen ist dieselbe wie das vorherige Wahr/Falsch-ODER-Wahrheitslayout (Tabelle).

Die NOT-Gleichung lautet:

A = Q

Wobei Q = A und der Balken über A bedeutet hier Komplement. Das Komplement von 0 ist 1 und das Komplement von 1 ist 0. Das NICHT-Gatter wird auch als INVERTIERENDES Gatter bezeichnet.

Dies sind die grundlegenden (oder Wurzel-)Wahrheitstabellen und ihre Gatter (kleine Schaltkreise) in der digitalen Elektronik (mit Boolescher Algebra). Die anderen drei Wahrheitstabellen, die in der folgenden Abbildung angegeben sind, und ihre Tore dienen der Vereinfachung und basieren auf den vorherigen drei Wahrheitstabellen.

Es gibt eine Wahrheitstabelle und ein Gatter, die aus der UND-Wahrheitstabelle und dem Gatter abgeleitet sind. Sie werden als NAND-Wahrheitstabelle (für NICHT UND) und als entsprechendes NAND-Gatter bezeichnet. Die NAND-Wahrheitstabelle und ihr NAND-Gatter sind:

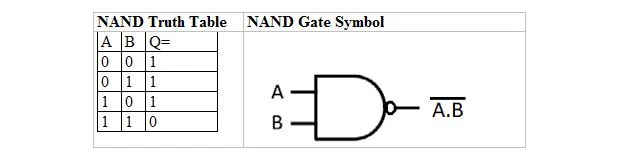
Um die NAND-Wahrheitstabelle zu erhalten, gehen Sie zur Ausgabe der AND-Wahrheitstabelle und ersetzen Sie jede Ziffer durch ihr Komplement. Das Komplement von 0 ist 1 und das Komplement von 1 ist 0. Das NAND-Gatter ähnelt dem UND-Gatter, hat jedoch einen kleinen Kreis vor der Ausgangsleitung. Die NAND-Gleichung lautet:

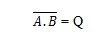
Wobei das Komplement des Ergebnisses von „A“ UND „B“ bedeutet. Der Balken (Overline) wird im Tor durch den kleinen Kreis dargestellt. Beachten Sie, dass der Punkt zwischen A und B weggelassen werden kann.

Es gibt eine weitere Wahrheitstabelle und ein weiteres Gatter, die von der ODER-Wahrheitstabelle und dem Gatter abgeleitet sind. Sie werden als NOR-Wahrheitstabelle (für NOT OR) und als entsprechendes NOR-Gatter bezeichnet. Die NOR-Wahrheitstabelle und ihr NOR-Gatter sind:

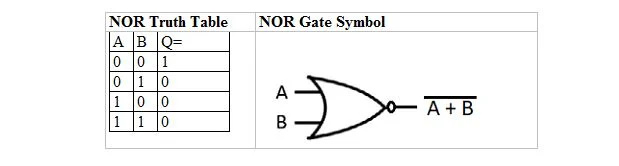
Um die NOR-Wahrheitstabelle zu erhalten, gehen Sie zur Ausgabe der ODER-Wahrheitstabelle und ersetzen Sie jede Ziffer durch ihr Komplement. Das Komplement von 0 ist 1 und das Komplement von 1 ist 0. Das NOR-Gatter ähnelt dem ODER-Gatter, hat jedoch einen kleinen Kreis vor der Ausgangsleitung. Die NOR-Gleichung lautet:

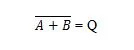
Wo 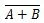bedeutet das Komplement des Ergebnisses von „A“ ODER „B“. Der Balken (Overline) wird im Tor durch den kleinen Kreis dargestellt.

Exklusives ODER (XOR)
Die Wahrheitstabelle für das ODER-Gatter lautet:

Im normalen Englisch ist nicht klar, ob die letzte Zeile von 1 OR 1 1 oder 0 ergeben soll. In der Booleschen Algebra gibt es also zwei Arten von OR-Wahrheitstabellen und zwei entsprechende Gatter. Beim normalen ODER ergibt die letzte Zeile von 1 ODER 1 1. Die andere Art von ODER ist das Exklusiv-ODER (XOR), bei dem die ersten drei Zeilen mit den ersten drei Zeilen des normalen ODER identisch sind (einschließlich Ausgabe). Für die vierte und letzte Zeile ergibt 1 ODER 1 jedoch 0.

Die folgende Tabelle enthält die XOR-Wahrheitstabelle und ihr XOR-Gatter-Symbol (kleiner Schaltkreis):

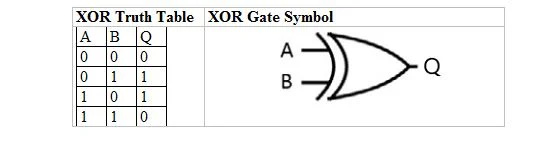
Sowohl für die XOR-Wahrheitstabelle als auch für ihr Gatter sind „A“ und „B“ zwei Eingabevariablen. „Q“ ist die Ausgangsvariable.

Die XOR-Gleichung lautet:

A ⊕ B = Q

Wobei das ⊕ hier Boolesches XOR bedeutet.

Das normale ODER bedeutet entweder oder beides. Exklusives ODER bedeutet streng entweder und nicht beides.

2.3 Boolesche Postulate

Postulate sind Annahmen, auf deren Grundlage bestimmte Schlussfolgerungen gezogen werden. Es gibt zehn boolesche Postulate, die auf den UND-, ODER- und NICHT-Gleichungen (Wahrheitstabellen) basieren. Diese Gleichungen werden auch Funktionen genannt. Die Grundfunktionen werden wie folgt nachgebildet:

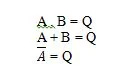
Dies sind die grundlegenden Funktionen (Gleichungen) in der Booleschen Algebra. Die folgenden anderen drei (Funktions-)Gleichungen sind keine Grundfunktionen:

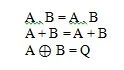
Obwohl die letzte Funktion hier eigenartig ist, wird sie nicht als grundlegende Funktion betrachtet.

Die booleschen Postulate lauten wie folgt:

Aus UND-Funktion
1) 0 . 0 = 0
zwanzig . 1 = 0
3) 1. 0 = 0
4) 1. 1 = 1

Aus ODER-Funktion
5) 0 + 0 = 0
6) 0 + 1 = 1
7) 1 + 0 = 1
8) 1 + 1 = 1

Von NOT-Funktion
9) 0 = 1
10) 1 = 0

Notiz: Bei diesen Postulaten handelt es sich lediglich um die Zeilen in den Wahrheitstabellen AND, OR und NOT, die auf unabhängige Weise ausgedrückt werden. Der Leser sollte sich die gegebenen Postulate merken.

2.4 Boolesche Eigenschaften

Eine Eigenschaft ist eine Eigenschaft von etwas. Boolesche Eigenschaften sind Gleichungen, die aus den booleschen Postulaten abgeleitet werden. In diesem Abschnitt werden die Eigenschaften einfach ohne ihre Ableitungen angegeben und anschließend verwendet. Es gibt 25 der Immobilien, die wie folgt in zehn Überschriften gruppiert sind:

Eigenschaften der UND-Funktion

Eigenschaft 1:

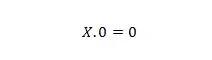
Dabei kann X 1 oder 0 sein. Das bedeutet, dass das Ergebnis unabhängig von X immer 0 ist.

Hinweis: Eine Variable muss nicht unbedingt A oder B oder C oder D sein. Eine Variable kann W oder X oder Y oder Z oder ein beliebiger anderer Buchstabe sein.

Eigenschaft 2:

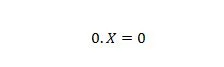
Dabei kann X 1 oder 0 sein. Beachten Sie, dass der Unterschied zwischen Eigenschaft 1 und Eigenschaft 2 darin besteht, dass auf der linken Seite des Gleichheitszeichens beider Gleichungen die Positionen von X und 0 vertauscht sind.

Eigenschaft 3:

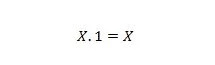
Wenn X 0 ist, dann 0. 1 = 0. Wenn X 1 ist, dann 1. 1 = 1.

Eigenschaft 4:

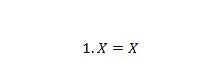
Wenn X 0 ist, dann ist 1. 0 = 0. Wenn X und 1 sind vertauscht.

Eigenschaften der OR-Funktion

Eigenschaft 5:

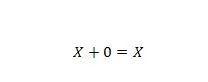
Dabei kann X 1 oder 0 sein. Das heißt, wenn X 0 ist, ist das Ergebnis 0. Wenn X 1 ist, ist das Ergebnis 1.

Eigenschaft 6:

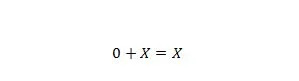
Dabei kann X 1 oder 0 sein. Beachten Sie, dass der Unterschied zwischen Eigenschaft 5 und Eigenschaft 6 darin besteht, dass auf der linken Seite beider Gleichungen die Positionen von X und 0 vertauscht sind.

Eigenschaft 7:

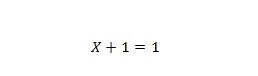
Wenn X 0 ist, dann 0 + 1 = 1. Wenn X 1 ist, dann 1 + 1 = 1.

Eigenschaft 8:

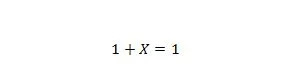
Wenn X 0 ist, dann ist 1 + 0 = 1. Wenn X und 1 sind vertauscht.

Eigenschaften bezüglich der Kombination einer Variablen mit sich selbst oder ihrem Komplement

Eigenschaft 9:

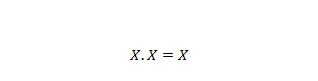
Das heißt: Wenn X 0 ist, dann 0 . 0 = 0. Wenn X 1 ist, dann 1 . 1 = 1.

Eigenschaft 10:

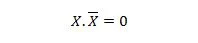
Das heißt: Wenn X 0 ist, dann 0. 1 = 0. Wenn X 1 ist, dann 1. 0 = 0.

Für aufeinanderfolgende Variablen wird diese Eigenschaft zu:

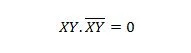
Eigenschaft 11:

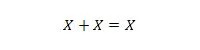
Das heißt: Wenn X 0 ist, dann 0 + 0 = 0. Wenn X 1 ist, dann 1 + 1 = 1 (aus dem normalen ODER).

Eigenschaft 12:

Das heißt: Wenn X 0 ist, dann 0 + 1 = 1. Wenn X = 1, dann 1 + 0 = 1.

Das heißt: Wenn X 0 ist, dann 0 + 1 = 1. Wenn X = 1, dann 1 + 0 = 1.

Doppelte Komplementierung

Eigenschaft 13:

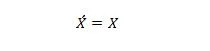
Wenn X auf der linken Seite 0 ist, wird X auf der rechten Seite 0. Wenn X auf der rechten Seite 1 ist, wird X auf der linken Seite 1. Mit anderen Worten: Doppelkomplemente geben den ursprünglichen Wert zurück.

Kommutativgesetz

Eigenschaft 14:

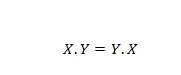
Das bedeutet, dass das Vertauschen des ersten und des zweiten Operanden für den UND-Operator auf der linken Seite des Gleichheitszeichens keine Rolle spielt; Die Antwort ist immer noch dieselbe, nachdem der Austausch auf der linken Seite stattgefunden hat. Diese Gleichung kann unter Weglassen der Punkte wie folgt geschrieben werden: XY = YX.

Eigenschaft 15:

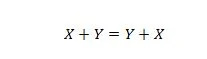
Die Erklärung hier ist die gleiche wie im vorherigen AND, gilt jedoch für den OR-Operator.

Verteilungsrecht

Eigenschaft 16:

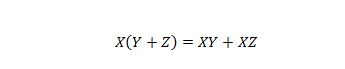
Hier gibt es drei Variablen: X, Y und Z. Jede Variable kann entweder 1 oder 0 sein. Auf der linken Seite des Gleichheitszeichens bedeuten die Klammern, dass zuerst ausgewertet werden soll, was darin steht. Dann ist AND das Ergebnis mit X. Die rechte Seite besagt, dass X UND Y zusammen ODER X UND Z zusammen dasselbe sind wie die linke Seite. Beachten Sie, dass der Punktoperator für die UND-Verknüpfungen durchgehend weggelassen wird; und die verknüpften Variablen bedeuten immer noch UND.

Eigenschaft 17:

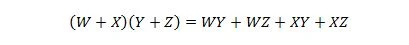
Diese Eigenschaft ist eine Erweiterung von Eigenschaft 16 mit der hinzugefügten Variablen W.

Assoziatives Recht

Eigenschaft 18:

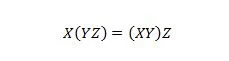
Klammern bedeuten, dass zuerst ausgewertet wird, was in den Klammern steht. Wenn also für den Ausdruck auf der linken Seite zuerst Y mit Z UND-verknüpft werden und X mit dem Ergebnis UND-verknüpft wird, dann ist das Endergebnis auf der linken Seite dasselbe wie das Endergebnis auf der rechten Seite -Handseite, wobei zuerst X mit Y UND-verknüpft wird, bevor das Ergebnis mit Z UND-verknüpft wird. Beachten Sie, dass die Punkte in der Gleichung weggelassen wurden.

Eigenschaft 19:

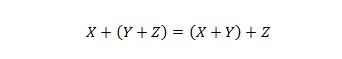
Diese Eigenschaft wird auf ähnliche Weise wie Eigenschaft 18 erklärt, jedoch wird anstelle des UND-Operators der ODER-Operator verwendet. Der Einfachheit halber wird der ODER-Operator + niemals in einem booleschen Ausdruck weggelassen. Andererseits kann der UND-Operator weggelassen und die beiden Variablen verknüpft werden.

Absorption

Eigenschaft 20:

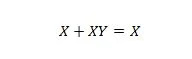
Bei dieser Gleichung ist die rechte Seite unabhängig von Y immer X (absorbiert).

Eigenschaft 21:

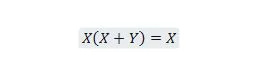
Außerdem ist bei dieser Gleichung unabhängig von Y die rechte Seite immer X (absorbiert). Diese Eigenschaft 21 ist die gleiche wie Eigenschaft 20, nämlich:

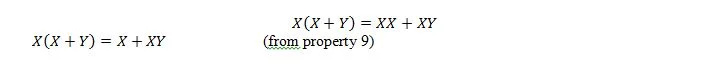
Hier nutzen wir das Verteilungsgesetz und die Tatsache, dass X.X = X der Eigenschaft 9.

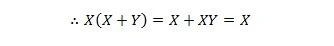
Eine Identität

Eigenschaft 22:

Dies bedeutet, dass für den X + Y-Ausdruck das Komplement von X vor Y den Ausdruck nicht ändert.

Eigenschaft 23:

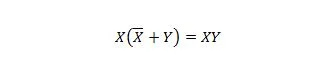
Dies bedeutet, dass für den XY-Ausdruck das zuerst durchgeführte Komplement von X ODER mit Y in Klammern den XY-Ausdruck nicht ändert.

DeMorgans Gesetz

Eigenschaft 24:

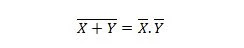
Dies bedeutet, dass ein NOR-Gatter (NOT OR) das gleiche Ergebnis hat wie das NOT-Verknüpfen der beiden Eingänge vor dem AND-Verknüpfen.

Eigenschaft 25:

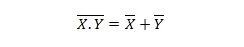
Dies bedeutet, dass ein NAND-Gatter (NOT AND) das gleiche Ergebnis hat wie die NOT-Verknüpfung der beiden Eingänge vor der ODER-Verknüpfung.

Die bereitgestellten Abbildungen zeigen die 25 Eigenschaften. Sie können bewiesen werden, indem alle verschiedenen möglichen Werte von Einsen und Nullen in jedem Ausdruck auf der linken Seite eingesetzt werden, um zu sehen, ob der Ausdruck (oder das Ergebnis) auf der rechten Seite erhalten wird. Die Beweise werden dem Leser als Übung überlassen.

2.5 Vereinfachung zusammengesetzter Ausdrücke

Die folgenden zwei Funktionen sind gleich:

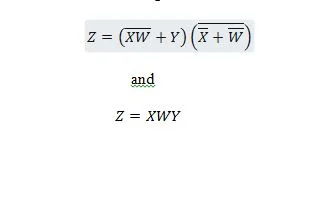
Z ist die Ausgabe und X, W und Y sind die Eingaben. Das erste benötigt ein NAND-Gatter, ein ODER-Gatter, ein UND-Gatter, zwei NICHT-Gatter, ein ODER-Gatter und ein NOR-Gatter. Der zweite benötigt nur zwei UND-Gatter. Die erste ist eine Gleichung mit einem zusammengesetzten Ausdruck auf der rechten Seite, der auf den einzigen Ausdrucksterm auf der rechten Seite für die zweite Gleichung vereinfacht (reduziert) wurde.

Eine Vereinfachung oder Reduzierung führt zu einer geringeren Anzahl von Gattern, um die gleiche Funktion wie eine Schaltung zu implementieren. Ein solcher kleinerer Schaltkreis kann Teil eines integrierten Schaltkreises (IC) oder ein eigenständiger Schaltkreis auf der Oberfläche der Hauptplatine des Computers sein.

Wenn eine Funktion (Gleichung) im Entwurfsprozess ankommt, muss eine Vereinfachung vorgenommen werden, um die Anzahl der Gatter zu reduzieren und am Ende eine kostengünstigere Schaltung zu erhalten. Die Vereinfachung erfordert die Verwendung einer oder mehrerer der vorherigen fünfundzwanzig booleschen Eigenschaften.

Beispiel 2.51:

Reduzieren Sie die Gleichung:

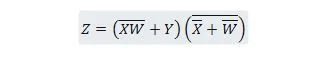
Notiz: Zwei Klammern nebeneinander bedeuten, dass die Klammern UND-verknüpft sind (der Punkt dazwischen wurde optional nicht geschrieben).

Lösung:
Bei den Lösungen wird jeweils rechts neben dem Schritt in Klammern die Begründung (Begründung) angegeben. Der Leser sollte jeden Schritt und seine Begründung lesen. Der Leser sollte sich beim Lesen der Funktionsreduktionsschritte auch auf die vorherigen Eigenschaften beziehen.

Beispiel 2.52:

Vereinfachen:

2.6 Mindestsumme der Produkte

Die folgenden zwei Funktionen sind gleich:

Beide Ausdrücke auf der rechten Seite beider Gleichungen liegen in der Form der Produktsumme (SP) vor. Ein Express-Ausdruck liegt in der Form „Produktsumme“ vor, wenn er keine Klammern enthält. Es ist offensichtlich, dass die erste Funktion (Gleichung) mehr Gatter benötigt als die zweite Funktion.

Der erste rechte Ausdruck kann noch reduziert werden, um die zweite Funktion zu erhalten. Der zweite Ausdruck auf der rechten Seite kann nicht weiter vereinfacht und dennoch als Summe von Produkten („Hinzufügen“ von Begriffen) ausgedrückt werden. Der zweite Ausdruck auf der rechten Seite kann nicht wirklich weiter vereinfacht werden. Es handelt sich also um ein MSP-Format (Minimum Sum of Products).

Beispiel 2.61:
Bringen Sie die folgende Funktion zuerst in das Formular „Summe der Produkte“ und dann in das Formular „Mindestsumme der Produkte“.

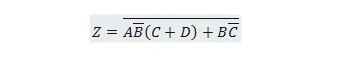
Lösung:
Bei der Lösung solcher Probleme müssen eine oder mehrere der vorherigen fünfundzwanzig Eigenschaften verwendet werden, wie in dieser Lösung dargestellt:

2.6 Mindestsumme der Produkte

Die folgenden zwei Funktionen sind gleich:

Beide Ausdrücke auf der rechten Seite beider Gleichungen liegen in der Form der Produktsumme (SP) vor. Ein Express-Ausdruck liegt in der Form „Produktsumme“ vor, wenn er keine Klammern enthält. Es ist offensichtlich, dass die erste Funktion (Gleichung) mehr Gatter benötigt als die zweite Funktion.

Der erste rechte Ausdruck kann noch reduziert werden, um die zweite Funktion zu erhalten. Der zweite Ausdruck auf der rechten Seite kann nicht weiter vereinfacht und dennoch als Summe von Produkten („Hinzufügen“ von Begriffen) ausgedrückt werden. Der zweite Ausdruck auf der rechten Seite kann nicht wirklich weiter vereinfacht werden. Es handelt sich also um ein MSP-Format (Minimum Sum of Products).

Beispiel 2.61:
Bringen Sie die folgende Funktion zuerst in das Formular „Summe der Produkte“ und dann in das Formular „Mindestsumme der Produkte“.

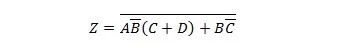
Lösung:
Bei der Lösung solcher Probleme müssen eine oder mehrere der vorherigen fünfundzwanzig Eigenschaften verwendet werden, wie in dieser Lösung dargestellt:

Dieser letzte Ausdruck liegt in der Form der Produktsumme (SP) vor, jedoch nicht in der Form der minimalen Produktsumme (MSP). Der erste Teil der Frage wurde beantwortet. Die Lösung für den zweiten Teil lautet wie folgt:

Diese letzte vereinfachte Funktion (Gleichung) liegt in MSP-Form vor und benötigt für die Implementierung weniger Gatter als die entsprechende SP-Form. Denken Sie daran: SP bedeutet Summe der Produkte, während MSP die Mindestsumme der Produkte bedeutet.

Beispiel 2.62:
Die folgende Schaltung verfügt über die Eingänge X, Y und W und Z ist der Ausgang. Erzeugen Sie die Funktion der Produktsumme (SP) (scheinbare Funktion der minimalen Produktsumme) für Z. Erzeugen Sie dann die tatsächliche, stärker reduzierte (minimierte) Produktsumme (MSP). Implementieren Sie dann die MSP-Schaltung (zeichnen Sie das MSP-Gating-Netzwerk).

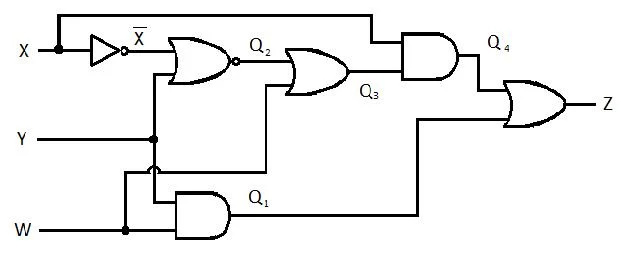
Abb. 2.61 Eine Torschaltung

Lösung:
Bevor der Vereinfachungsprozess beginnt, muss der Ausdruck für Z in Form von X, Y und W ermittelt werden. Sehen Sie sich diese Beispielillustration aus dem Diagramm an:

Dies ist der Ausdruck von Z in Form von X, Y und W. Danach kann die Vereinfachung zum scheinbaren MSP erfolgen. Anscheinend ist MSP SP.

Diese letzte Gleichung (Funktion) liegt in SP-Form vor. Es handelt sich nicht um die Mindestsumme der Produkte (noch nicht MSP). Die Reduzierung (Minimierung) muss also weitergehen.

Diese letzte Gleichung (Funktion) ist eine echte minimale Produktsumme (MSP). Und die Gating-Schaltung für die minimale Produktsumme (echte Minimierung) ist:

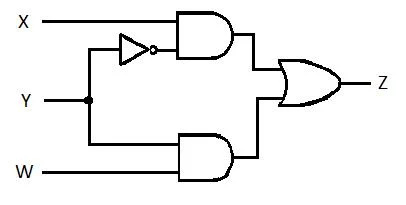
Abb. 2.62 MSP-Gating-Schaltung

Kommentar
Aus der Analyse in diesem Abschnitt geht hervor, dass nicht klar ist, ob die Summe der Produkte die Mindestsumme der Produkte ist oder nicht. SP ist nicht sehr nützlich. Es ist MSP, das sehr nützlich ist. Es gibt einen sicheren Weg, MSP zu erhalten; Es ist die Karnaugh-Karte zu verwenden. Karnaugh Map geht über den Rahmen dieses Online-Karrierekurses hinaus.

2.7 Probleme

Dem Leser wird empfohlen, alle Probleme in einem Kapitel zu lösen, bevor er mit dem nächsten Kapitel fortfährt.

1. Erstellen Sie die Wahrheitstabellen UND, ODER und NICHT mit den entsprechenden Gattern.
2. Schreiben Sie die zehn Booleschen Postulate in ihren verschiedenen Kategorien auf und benennen Sie die Kategorien.
3. Schreiben Sie ohne Erklärung die 26 Eigenschaften der Booleschen Algebra in ihren verschiedenen Kategorien auf und benennen Sie die Kategorien.
4. Reduzieren Sie die Gleichung mithilfe der booleschen Eigenschaften und unter Angabe der verwendeten Kategorien.



5. Reduzieren Sie die Gleichung mithilfe der booleschen Eigenschaften und unter Angabe der verwendeten Kategorien.



6. Reduzieren Sie mithilfe der booleschen Eigenschaften und unter Angabe der verwendeten Kategorien die folgende Gleichung – zuerst auf die Summe der Produkte und dann auf die minimale Summe der Produkte:



7. Reduzieren Sie mithilfe der booleschen Eigenschaften und unter Angabe der verwendeten Kategorien die folgende Gleichung – zuerst auf die Summe der Produkte und dann auf die minimale Summe der Produkte: